
NPTEL Course a fun filled whirlwind tour of 30 hrs, covering everything you need to know to fall in love with the most sought after skill of the 21st century. The course brings programming to your desk with anecdotes, analogies and illustrious examples. Turning abstractions to insights and engineering to art, the course focuses primarily to inspire the learner’s mind to think logically and arrive at a solution programmatically. As part of the course, you will be learning how to practice and culture the art of programming with Python as a language. At the end of the course, we introduce some of the current advances in computing to motivate the enthusiastic learner to pursue further directions. The Joy of Computing using python is a fun filled course offered by NPTEL.
The Joy Of Computing Using Python Week6 Assignment Jan 2024
INTENDED AUDIENCE : Any interested audience
PREREQUISITES : 10th standard/high school
INDUSTRY SUPPORT : Every software company is aware of the potential of a first course in computer science. Especially of a first course in computing, done right.
Course Layout
- Motivation for Computing
- Welcome to Programming!!
- Variables and Expressions : Design your own calculator
- Loops and Conditionals : Hopscotch once again
- Lists, Tuples and Conditionals : Lets go on a trip
- Abstraction Everywhere : Apps in your phone
- Counting Candies : Crowd to the rescue
- Birthday Paradox : Find your twin
- Google Translate : Speak in any Language
- Currency Converter : Count your foreign trip expenses
- Monte Hall : 3 doors and a twist
- Sorting : Arrange the books
- Searching : Find in seconds
- Substitution Cipher : What’s the secret !!
- Sentiment Analysis : Analyse your Facebook data
- 20 questions game : I can read your mind
- Permutations : Jumbled Words
- Spot the similarities : Dobble game
- Count the words : Hundreds, Thousands or Millions.
- Rock, Paper and Scissor : Cheating not allowed !!
- Lie detector : No lies, only TRUTH
- Calculation of the Area : Don’t measure.
- Six degrees of separation : Meet your favourites
- Image Processing : Fun with images
- Tic tac toe : Let’s play
- Snakes and Ladders : Down the memory lane.
- Recursion : Tower of Hanoi
- Page Rank : How Google Works !!
Programming Assignment 1
Question 1 : The distance between two letters in the English alphabet is one more than the number of letters between them. Alternatively, it can be defined as the number of steps needed to move from the alphabetically smaller letter to the larger letter. This is always a non-negative integer. For example:
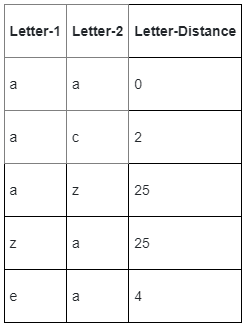
The distance between two words is defined as follows:
- It is -1, if the words are f unequal lengths.
- If the word-lengths are equal, it is the sum of the distances between letters at corresponding positions in the words. For example:
dword(dog,cat)=dletter(d,c)+dletter(o,a)+dletter(g,t)=1+14+13=28
Write a function named distance that accepts two words as arguments and returns the distance between them.
You do not have to accept input from the user or print output to the console. You just have to write the function definition.
def distance(word_1, word_2):
"""
calculate the distance between two words
Argument:
word1: str
word2: str
Return:
dist: int
"""
if len(word_1) != len(word_2):
return -1
dist = sum(abs(ord(w1) - ord(w2)) for w1, w2 in zip(word_1, word_2))
return dist
Programming Assignment 2
Question 2 : P is a dictionary of father-son relationships that has the following structure: for any key in the dictionary, its corresponding value is the father of key. As an example:
P = {
‘Jahangir’: ‘Akbar’,
‘Akbar’: ‘Humayun’,
‘Humayun’: ‘Babur’
}
If ‘Jahangir’ is the key, then ‘Akbar’, his father, is the value. This is true of every key in the dictionary.
Write a recursive function named ancestry that accepts the following arguments:
- P: a dictionary of relationships
- present: name of a person, string
- past: name of a person, string
It should return the sequence of ancestors of the person named present, traced back up to the person named past. For example, ancestry(P, ‘Jahangir’, ‘Babur’) should return the list:
L = [‘Jahangir’, ‘Akbar’, ‘Humayun’, ‘Babur’]
In more Pythonic terms, L[i] is the father of L[i – 1], for 1≤ i < len(L), with the condition that L[0] should be present and L[-1] should be past.
(1) You can assume that no two persons in the dictionary have the same name. However, a given person could either appear as a key or as a value in the dictionary.
(2) A given person could appear multiple times as one of the values of the dictionary. For example, in test-case-2, Prasanna has two sons, Mohan and Krishna, and hence appears twice (as a value).
(3) You do not have to accept input from the user or print output to the console. You just have to write the function definition.
def ancestry(P, present, past):
"""
A recursive function to compute the sequence of ancestors of person
Arguments:
P: dict, key and value are strings
present: string
past: string
Return:
result: list of strings
"""
if present == past:
return [present]
else:
return [present] + ancestry(P, P[present], past)
Programming Assignment 3
Question 3 : Fibonacci
Fibonacci is a young resident of the Italian city of Pisa. He spends a lot of time visiting the Leaning Tower of Pisa, one of the iconic buildings in the city, that is situated close to his home. During all his visits to the tower, he plays a strange game while climbing the marble steps of the tower.
The Game
Fibonacci likes to climb the steps either one at a time, two at a time, or three at a time. This adds variety to the otherwise monotonous task of climbing. He wants to find the total number of ways in which he can climb n steps, if the order of his individual steps matters. Your task is to help Fibonacci compute this number.
For example, if he wishes to climb three steps, in the case of n=3, he could do it in four different ways:
- (1,1,1) (1,1,1): do it in three moves, one step at a time
- (1,2) (1,2): do it in two moves, first take a single step, then a double step
- (2,1) (2,1): do it in two moves, first take a double step, then a single step
- (3): do it in just one move, directly leaping to the third step
To take another example, if n=5, then some of the sequences could be:
(1,3,1), (1,1,3), (3,1,1), (2,1,1,1), (1,2,1,1), (2,1,2)
Each sequence is one of the ways of climbing five steps. The point to note here is that each element of a sequence can only be 1, 2, or 3.
Write a recursive function named steps that accepts a positive integer n as the argument. It should return the total number of ways in which Fibonacci can ascend n steps. Note that the order of his steps is important.
You do not have to accept input from the user or print output to the console. You just have to write the function definition.
def steps(n):
"""
A recursive function to compute the number of ways to ascend steps
Argument:
n: integer
Return:
result: integer
"""
if n == 0:
return 1
elif n < 0:
return 0
else:
return steps(n-1) + steps(n-2) + steps(n-3)